 First things first,1 never buy a lottery ticket. Seriously, ever.
First things first,1 never buy a lottery ticket. Seriously, ever.
Having said that, obviously I did buy a few this past week because, you know, I’m an irrational human.
I’ll be the first to admit it. I also sometimes buy “King Size” Reese’s peanut butter cups (that’s the four-in-one size) in the checkout line at the grocery store and, man, they’re gone by the time I make it to the car. So, I allow myself bad decisions from time to time.
But this is not confession-time with Mike. Rather, it’s financial math-time, with a Powerball lottery theme.
A friend asked me over Facebook whether it made more sense (when he wins the whole shebang this week) to take the lump sum or 30 annual payments.

What I’m not analyzing
Now, I can think of lots of valid ways to answer the annuity versus lump sum question, and I’m going to skip most of these to focus simply on the mathematical way to think about it. In that sense, I will be simplifying the issue terribly – disregarding factors such as personal circumstance, economic utility, needs and wants of heirs and recipients, current and future rates of taxation, variations on self-control, and personal health/longevity. I only want to use the example of the lottery to illustrate some important financial mathematics.
And before you decide to skip the math analysis (because math is soooo boring, blah blah blah), just know that this math formula is the basis for ALL fundamental investing – All bond analysis, all stock analysis, all real estate investing, all business investments. Everything. If you don’t use this math, you’re just guessing. Well, even if you do use this math, you still may be guessing, but you’re guessing less than you would have guessed without the math.
The math is called “Discounting Cashflows,” and probably by now you’ll have wised up to the fact that I’m piggy-backing on the Powerball lottery story to slip in a lesson on what forms part of the most powerful financial math in the universe.
So like I said, I’m skipping whether you think you’ll live for another 30 years and whether that makes you want to gratify your material wants this year. I’m skipping the issue of taxes partly because we don’t know what tax rates will be like over the next thirty years, and also because taxes are part of the reason why lotteries in particular are a mug’s game.2 I’m skipping the issue of squandering all the money3 this year versus stretching out your squander over 30 years. I’m skipping whether you have great philanthropic desires that may be satisfied this year or in later years when you (finally!) acquire more maturity and thoughtfulness.
Ok, with all that throat-clearing and telling you what I won’t analyze, let’s move to the mathematical issue of:
Annuity versus lump sum
What the math explained below can tell you, precisely, is whether a lump sum today is worth more or less than a 30-year annuity payout, given your % return assumptions.
To properly compare your lump sum option today to the 30 annual payments option, you first have to assume a % annual ‘return’ that you would expect to be capable of generating those annual payments.
Introducing: “Discount Rate”
The assumed “% annual return” I mentioned in the previous sentence goes by a couple of different names when you do this math. The alternate names include Annual Return, IRR (Internal Rate of Return), or Yield. The best math name for this particular situation is Discount Rate, but in practice it ends up meaning the same thing as those other names.
How do we come up with an assumed Discount Rate? There’s some art here as well as science, and a useful Discount Rate for this situation adds up factors such as inflation, prevailing interest rates, and the riskiness of each annuity payment. Without getting into a tangential detour about coming up with the ‘right’ number for the ‘Discount Rate,’ on lottery payments4, I’ll just grab one for now and move on to showing the math. Let’s call the right Discount Rate on future annuitized lottery payment 3%.5
Discounting future cash flows
Money arriving one year from now – or 30 years from now – is always worth less to me than money in my bank account today.6 We can understand this intuitively by thinking about the fact that you can’t literally buy beer and a hamburger today with money promised to you one year from now. Also, in one year, or thirty years, your circumstances may change, which would make you value money in your bank today above money owed to you in the future. Also, future promises are inherently risky. What if the person owing the money, or the lottery commission for that matter, never pays you in the future? What if inflation reduces the purchasing power of the future money? For all these reasons, we say that money today is worth more than the same (aka ‘nominal’) amount of money in the future.
But how much more? The point of discounting future cash flows mathematically is to turn that intuition I describe in the prior paragraph into a precise number telling me ‘how much more’ I value today’s money than future promised money.
This is the heart of comparing my lottery lump sum to a series of 30 annual payments. It’s also the heart of figuring out how much money I’ll earn if I buy a bond at a set price, or a stock at a set price, or a rent-generating piece of commercial real estate, or a profitable business. In essence, in each of these situations, I’m asking how much would I pay today to generate a series of future payments, at a given assumed rate of return?
Would you just tell me the math already? Geez!
Ok, fine. Let’s say you win the total Powerball payout this week (as of this writing) of $1.5 Billion. And let’s say the annuity deal is you can receive 30 equal payments of 50 million each year7, starting one year from now.8 And let’s say the lump sum offer today (as of this writing) is $930 million. Which one is worth more, the lump sum or the 30 annuitized payments?
Our math challenge is to ‘discount’ each of those 30 payments of $50 million into an equivalent value in today’s dollars. That consists of 30 different calculations. What is $50 million – one year from now – worth today? What is $50 million – 5 years from now – worth today? For that matter, what is $50 million – arriving thirty years from now – worth today?
Each of the separate 30 annuity payments gets discounted separately. Mathematically, 1 year from now is different from 2 years from now which is different from 30 years from now. For simplicity’s sake, I’m going to stick with a single Discount Rate – the same 3% – for each future payment.9 Also, to do this right, you’ll want to open up a spreadsheet right about now. If you are mildly competent with Excel,10 you can follow the math below by creating the following formula, and then reproducing the formula thirty times, one for each year’s annuity payment. And if you are mildly comfortable with Excel, the reproducing of the formula part should take you about 12 seconds. It’s an autofill function.
A little Algebra
Sorry about this, but I’m going to mention some algebra. This won’t hurt a bit. Just hold your breath, and…The algebra formula for discounting any future payment into today’s money is PV = FV/(1+Y)^N. Don’t worry, I’ll define everything…Ok, release breath. Phew.
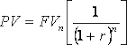
In that formula PV (Present Value) means the value of money today (which is what you want to solve for, in order to compare with the lump sum), and FV means the Future Value of the annuity payment, which in the case of the Powerball example we’ve said is $50 million.
Also in that formula Y is what I’m using for the Discount Rate, which I’ve decided for the time being is 3%. And N is the number years from now that the future payment arrives.
So, to discount a Powerball annuity payment arriving one year from now I’d say that the Present Value (PV) is equal to $50 million/(1+3%)^1. Which, my Excel spreadsheet tells me, is $48,539,758. In plainer English, I should equally value $48,539,758 today, or $50 million set to arrive one year from now.11
To discount a Powerball annuity payment arriving two years from now I’d say that the Present Value (PV) is equal to $50 million/(1+3%)^2. Which, my Excel spreadsheet tells me, is $47,125,979. In plainer English, I should equally value $47,125,979 today, or $50 million set to arrive two years from now.
To give you a sense for the power of discounting, my Excel tells me that the $50 million payment arriving 30 years from now is equivalent to $20,585,997 in today’s money. You can check that math yourself by plugging in $50 million/(1+3%)^30 into Excel, or your calculator.
To solve the lump sum versus annuity question, I’d set up my Excel spreadsheet to give me a value for each of the thirty annuity payments of $50 million. Like I mentioned, this takes approximately 12 seconds for someone mildly comfortable with setting up formulas in Excel.
Once you have a value for each of the 30 payments, discounted to the present day (aka the Present Value of each of the 30 payments) then you add them all up, and compare them with the lump sum.
When I add up thirty annual payments of $50 million each, each discounted at a 3% Discount Rate between one and thirty years from now, I get a total value of $979,726,641.
Assuming my 3% Discount Rate is the right one, I can compare that value to the lump sum offer (which I mentioned above, and as of this writing) of $930 million. Since the bigger number is the sum of the annuitized payments, then I can say that the 30 annuitized payments are a ‘better deal,’ in pure financial terms, than the lump sum.
But notice something
The mathematical answer to the ‘lump sum versus annuity’ question depends entirely upon inputting a specific, assumed, Discount Rate. Change the Discount Rate, and the ‘correct’ answer changes.
If I assume a 4% Discount Rate, for example, the value of next year’s payment declines to $48,071,757 – because that’s $50 million/(1+4%)^1, and the sum of all annuity streams is only worth $864,271,673. At a 4% Discount Rate, the lump sum value of $930 million dwarfs the value of the annuity payments.
What would make the ‘correct’ Discount Rate change? In the case of guaranteed Powerball lottery payments, the most probable influence would be inflation. If the world suddenly expected 5% annual inflation for the next thirty years, for example, then the correct Discount Rate would be something above 5%, and the lump sum begins to look far more valuable than the annuity. On the other hand, low inflation and continued low interest rates would make the annuity payments relatively more valuable, because we could imagine inputting a Discount Rate even less than 3%.
Two other small points
By the way, I can set my programmed spreadsheet to tell me what the ‘Discount Rate’ is that the Powerball folks use, which turns out to be (if you use my assumptions) approximately 3.4%.12
The second small point is that if you know the Discount Rate that Powerball uses (like 3.4% in my example), you could reasonably say that your ‘investment hurdle’ for taking the lump sum is 3.4%. What I mean by that is that if you take the lump sum, and then can reliably compound an investment return on that money – not spending, just investing! – above 3.4% every year for the next 30, then you could end up with more money in the end than you would through the annuity option.
A reminder
Discounting cashflows only answers one aspect of the lump sum versus annuity question. Remember what I started out saying, which is that there are a ton of factors I’m not considering, in my interest in showing some elegant math. But at least we have a mathematical answer to the question of ‘should I take the sump sum or the annuity?’
An exhortation
I’m going to make up a statistic which, while not exactly true,13 is at least ‘truthy:’ Less than one person in a hundred understands how to do discounted cashflows math.
I believe deeply that everybody should understand discounting cashflows, in a ‘you should know this to be an adult in the world’ kind of way. Your bank understands this math and uses it to profit from transactions with you. Your insurance company uses this math when calculating your rates, and has a complete advantage over all its customers who cannot do this math. All of Wall Street is built entirely on the discounted cashflows formula.14
You really don’t need to understand the lump sum versus annuity question for this week’s Powerball. You do, however, need it for life.

Conclusion
Real talk time: You’re not going to win Powerball. Lotteries are terrible.
But if you managed to spend some time with a spreadsheet to compare the lump sum versus annuitized payout as a result of fantasizing about the Powerball drawing, well then I’d say you’ve gained something this week. And properly deployed, what you’ve gained by understanding discounting cash-flows math could – and I mean this totally in earnest – make you wealthy in the long run.
Learning this math – and not some lottery fantasy – will make you a winner this week.
Please see related posts:
Discounting Cashflows – The example of an annuity
Discounting cashflows – Golden parachute?
Longevity Insurance – Do You Feel Lucky?
Compound Interest – The Most Powerful Math in the Universe
Compound Interest – Your Credit Card Debt
Compound Interest – Get Rich Slow
Compound Interest – If You Like Feral Cats
Post read (22294) times.
- “…I’m the realest.” At least, that’s how I wanted to end the sentence. Because I’m So Fancy. ↩
- In other words, considering taxes will muddy up the elegant and essential mathematic point I’m trying to make. ↩
- Obviously I want to use the delightful phrase “on hookers and blow,” the proverbial natural beneficiaries of your squander. ↩
- Ok, I’ll indulge in a little tangent here. The biggest influence on a thirty-year lottery payment guaranteed by a state in the US is probably the expected rate of inflation. If you think the rate of inflation will average, say, 2% over the next 30 years, then most of the Discount Rate will be made up of this. The ‘risk’ of non-payment by a state-sponsored lottery commission is low. And yes, I’m ignoring you preppers who stock up on canned goods and ammo for the imminent implosion of constitutional order, who say the state will likely dissolve over the next 30 years, with federal fiat money replaced by Bitcoins. Whatever, dude. ↩
- Again, I’m not saying this is the ‘right’ Discount Rate, I’m just saying let’s pick a number so I can illustrate the math formula. Then you get to change the Discount Rate to whatever you want it to be, and come up with a different analysis of the relative merits of lump sum versus 30 years of annuity payments. ↩
- The concept in this paragraph is short-handed in finance circles as ‘The Time Value of Money.’ ↩
- By the way, it doesn’t matter for the math example, but the actual Powerball pays in increasing annuity amounts each year. So on a $1.5 Billion prize, presumably the initial payments are less than $50 million and the later payments exceed $50 million. But I’m going for simplicity here. ↩
- Also, technically, when you win Powerball you get an immediate lottery payment straight away, followed by 29 future years of annuity payments. So the math in real life varies a little bit from my example. But since nobody reading this will be winning, and playing Powerball is an exercise in fantasy anyway, I think it’s appropriate to disregard actual real-life technicalities in the interest of learning some math. ↩
- But you wouldn’t have to. If you had paranormal insight into some event happening 15 years from now (like Miley Cyrus gets elected President) and some resultant uptick in either inflation or just risk, you could build a simple math model that assumes 3% discount rate for the first 15 years, and then a 7% discount rate for years 16 through 30. Knock yourself out! Vote Cyrus! ↩
- Now that I’ve introduced Excel into my method, you clever Excel-using people are going to want to tell me about a shortcut for doing present value with fixed annuity payments at fixed intervals. But there is a method to my madness in explaining the ‘long way.’ That Excel shortcut can do annual and regular discounting fine, but is not as flexible as it should be for all cases of discounting future cashflows. Shortcuts won’t help you with irregular future cashflows that arrive at irregular times. Learning the discounted cashflows math the ‘long way,’ applicable for every case, is a far more valuable skill, in my opinion. ↩
- Important Note/Correction…A number of you did this math and found slightly different values. I should have clarified: When setting up my spreadsheet I always use actual dates of payment to generate the compounding period N. So for example I set up an original date of 1/1/16 and annuity payments made annually on 1/1/17, 1/1/18, etc. When you use actual dates you get an N of 366/365 (instead of 1) in 2016 (it’s a leap year) and the Actual#days/365. I didn’t clarify that in the original version of this post. Using a simple 1,2,3 etc for N isn’t wrong, It’s just I’m in the habit of using actual dates for investments and I did it this time without pointing it out. The good news: Some of you checked out the math with your spreadsheets! ↩
- Update: The NYTimes has a a good article in which the reporter notes the lottery uses an assumed Discount Rate – to convert $1.5Billion in annuity payments into a $930 million lump sum – of 2.843%. The Times guy, I believe, has access to – or figured out – the exact schedule of payments, which includes a schedule of increasing annual payments, rather than the equal payments like I used in my spreadsheet. My number assumes 30 equal payments in years 1 through 30, and the real schedule is an upfront payment immediately, followed by 29 increasing annuity payouts in years 1 through 29. Since I don’t know the exact increasing schedule of Powerball between years 1 through 29, I’m going to just stay focused on my math formula. ↩
- I have no idea what the true number is. ↩
- Well that, plus the immortal souls of unburnt sacrificial virgins. And coffee. Don’t forget coffee. ↩

